Finding Boggle Grid Scores

Posted by Andrew on February 9, 2017

If you haven’t read my last post, go ahead and read that before diving in here. It’s not strictly necessary, but it will give you some context.

In my last post discussing high scoring Boggle boards, I skipped over some important details. Because I wanted to keep my focus on the genetics aspect of the solution, I didn’t walk through actually scoring the boards. A few people have asked me about the details, so I thought it’d be fun to share that as well. If your recreational reading is solely focused on Boggle board solving, there are many resources out there for you as well beyond this post1 2 3, and I won’t be blazing any new trails here.

Here are the rules of Boggle for everyone who may have forgotten them since we last talked:

Boggle is played with a 4-by-4 grid of letters. Points are scored by finding strings of letters — connected in any direction, horizontally, vertically or diagonally — that form valid words at least three letters long. Words 3, 4, 5, 6, 7 or 8 or more letters long score 1, 1, 2, 3, 5 and 11 points, respectively.

And an example board:

Solution Approach

Our goal is to most efficiently find all the words of a given dictionary contained in a given grid of letters.

Let’s start by listing off criteria that our algorithm must meet:

  • Words can start on any letter.
  • The next letter in a word can be orthogonal or diagonal to the current letter.
  • A single letter cannot be used more than once in a word.
  • Words must be three or more letters.

Dictionary

In order to know what qualifies as a word, we need a dictionary to pull from. In this case, I’ll be using the public domain word list enable1.txt. It contains approximately 170,000 of the most commonly used words. There’s nothing special about this list, it just happens to be popular for this type of puzzle and public domain.

Searching The Grid

Naive

The most basic solution is to traverse all possible paths through the grid, only stopping when there are no more available squares to move to. Along the way, each string of letters would be checked to see if it’s a word. This approach would certainly be the the most thorough, but would also lead to countless unnecessary calculations.

For example, say the first four letters of a search path spell out XKCD. Using this naive strategy, the search would continue, checking for all possible words in the grid starting with XKCD. Because there are no words in our dictionary starting with XKCD, this is going to be fruitless, and that particular search path could have been stopped already. The naive search will spend a significant amount of time searching paths that can be eliminated as dead ends.

Additionally, this algorithm would construct every possible traversal of the grid, which would take quite a long time. Moving along a grid such as this, while not allowing for repeated stops at the same point is called a self-avoiding walk. For smaller grids such as this, it’s possible to enumerate all the paths, but a general formula doesn’t exist for an arbitrary grid size. (This enumeration would look similar to this if you’re wondering.)

Be More Selective

It makes sense for us to trim our search down to not pursue dead ends, but how? As the search progresses, we’ll check to see if the current string is a word, or there are any words in our list that starts with the string. If there doesn’t exist a word that starts with the string, stop searching that path and pick a new direction to search.

Smarter Lookups

Now that we know we’re going to be checking the dictionary frequently for prefixes, let’s explore ways to make that lookup faster.

Take a second to think about how you might check a dead tree dictionary for the word isopod. You would start at i, then move to is, etc. If your dictionary didn’t have any words that started with isop, then you know that isopod is not in your dictionary, and no further searching is needed.

Our algorithm (so far) is searching for prefixes by starting at the top of the list and searching the entire thing. This would equivalent to reading through every word in the dictionary looking for isopod. Probably not the best strategy.

In order to make the search more efficient, we’ll be transforming our dictionary into an ordered tree structure called a trie. Our trie will have nodes that represent a string of letters. The string is determined by adding together the letters from all the nodes that were traveled so far. Confused? How about an example.

Here is a trie representing the following words: a about above across act active activity cake call can candle keep key kill kin kind king. The boldly circled nodes represent the end of words.

A trie is great for this application because as you travel down the nodes of the tree, you’re constructing a word. As you search, if the next letter in your word doesn’t appear in the tree, you know that your word is not contained in the dictionary.

For example if we search for kin, we can find it by first searching for, then moving to the k, then the i, then the n. Because we ended our search in the tree, kin is in our dictionary.

Similarly for kind, we have the following search. Note however, that if we were to search for kindly, when we arrived at the d node, there would be no l node to travel to. Right away, we know that kindly was not one of our original words.

Putting it Together

Here is an animated example showing a grid being searched for our example dictionary words. The trie animation is color coded to help follow it. Keep in mind, we’re only searching for a select few words in this example.

  • red: the current word is not in the dictionary
  • yellow: there are still words that start with that string
  • green: we’ve found a word!

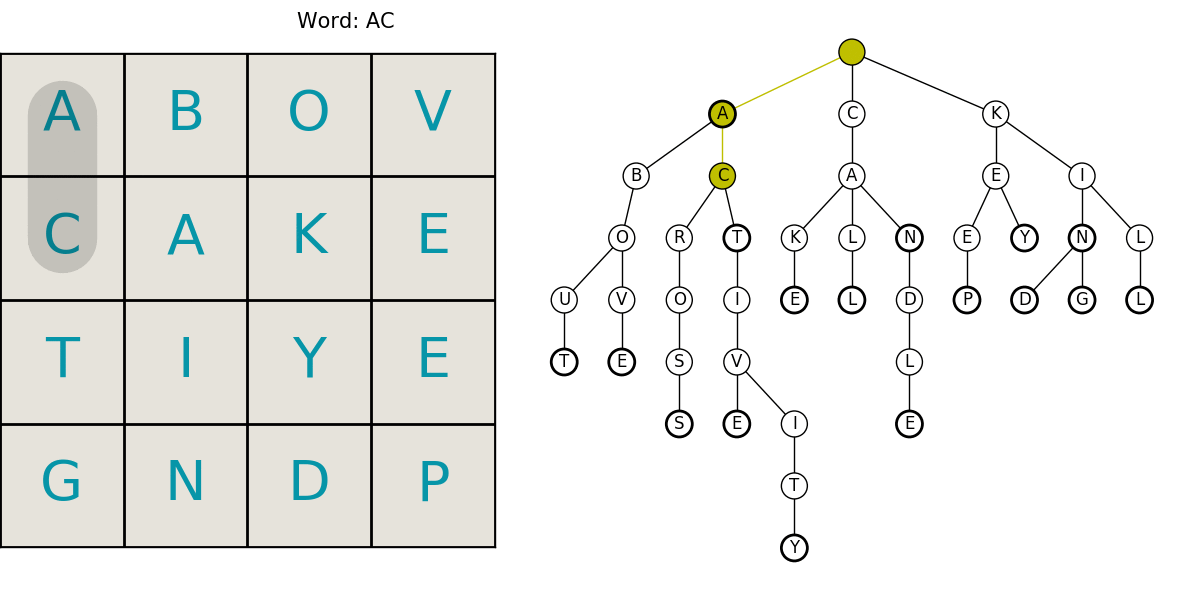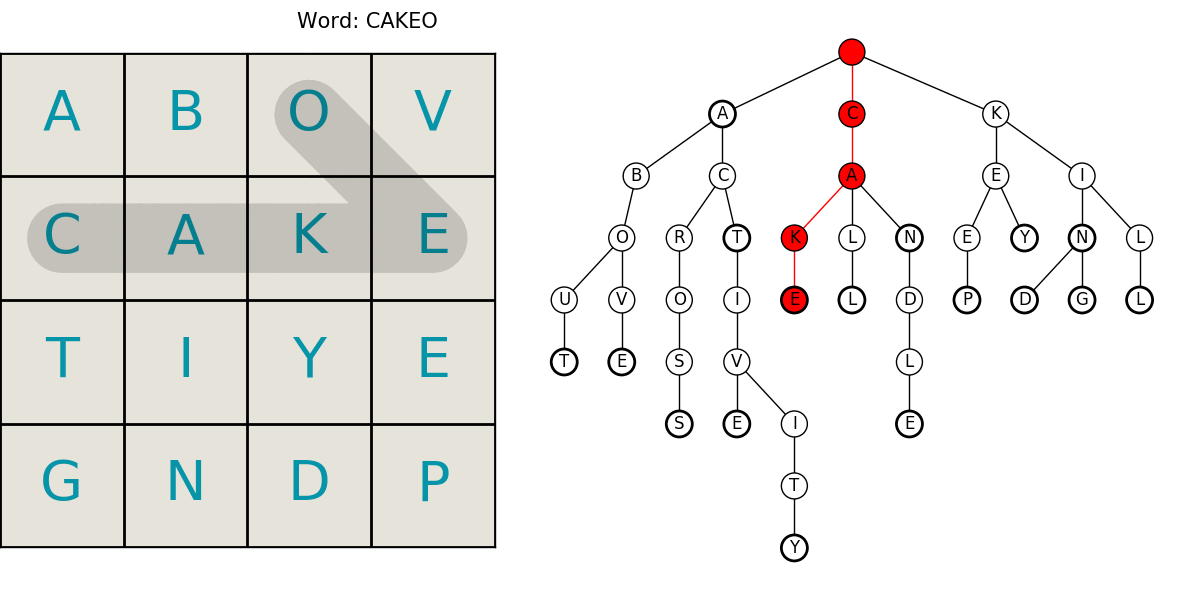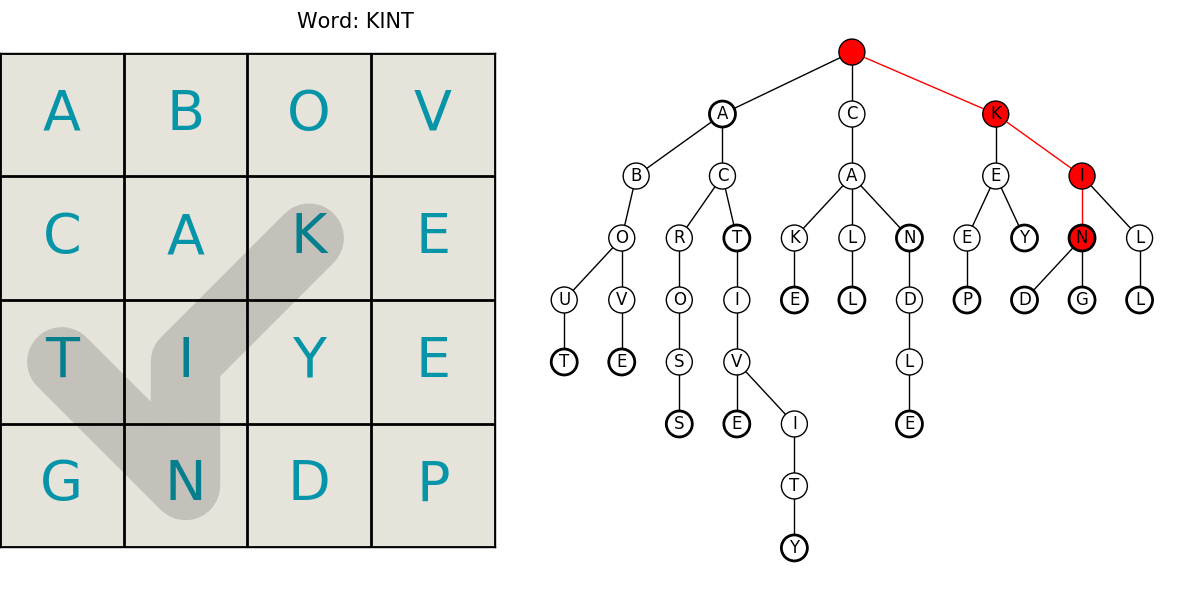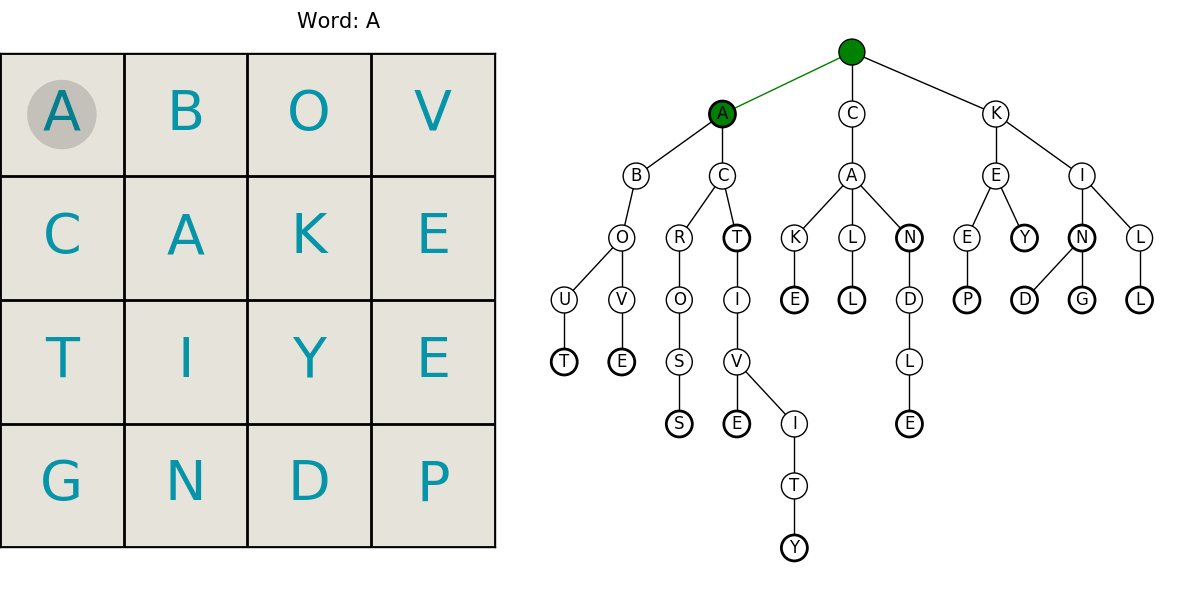
This neatly summarizes the entire process including the compact trie structure for efficient lookups in the dictionary, and the path searching. What follows is the code and a little more in-depth explanation of the algorithms. I hope you enjoyed it! Let me know if you find an error or have something interesting you want to hear about.

The Nitty Gritty

This is a selection of the important parts of code to perform the search. The full files can be found at: recurse_grid.pyx and boggle.py.

Constructing the Trie

The trie is constructed as a dict 4 in python. At the top level, the keys are the first letters of all the words. Inside each of those is another dict containing all the seconds letters of words that started with the first letter, etc. Additionally, because we want to find words that are contained within other words, there is a special key (END) that signals that the string ending on that node is a word itself. This makes sure that we both count that word, but also continue searching if it’s also a prefix to further words. Lastly, each node has a unique integer to aid in drawing the graphs later.

def make_trie(words):
    current_node_number = 0
    # start with an empty dictionary
    root = dict()
    # the base node will be node 0
    # each node will have a unique number assigned
    # to it that is used for drawing the graph later
    root[NUM] = current_node_number
    current_node_number += 1

    for word in words:
        # for each word, the addition of the letter nodes
        # needs to start at the root level again
        current_dict = root
        for letter in word:
            # if the node for this letter doesn't exist yet, create
            # and empty dictionary there
            if letter not in current_dict:
                current_dict[letter] = {}

            # as the letters get counted, traverse further into the dict
            # to add the nodes for all the letters
            current_dict = current_dict[letter]

            # if this node does not have a number already
            # add one and increment the counter
            if NUM not in current_dict:
                current_dict[NUM] = current_node_number
                current_node_number += 1

        # add the END key at the deepest node for this word
        # to signal that this string is a word.
        current_dict[END] = END
    return root

Searching the Trie

Once there is a candidate word, we need to check the trie to determine if it’s a word, a valid prefix to other words, or not a word (invalid). This function attempts to keep going deeper into the trie with each letter, until either:

  1. The search can’t find the next letter: invalid
  2. All letters are found. Then either,
    1. END is present: word
    2. END not present: prefix
class TrieMembership(IntEnum):
    invalid = 1
    prefix = 2
    word = 3


def trie_member(trie, word):
    # if the word has not been tested already, calculate whether the string
    # is not a valid word/prefix, whether it is a prefix to possible words
    # or a word itself.
    except KeyError:
        current_dict = trie
        for letter in word:
            try:
                # attempt to follow the letters through the trie dict
                current_dict = current_dict[letter]
            except KeyError:
                # once a key is not found, this means this word is not in the trie
                return TrieMembership.invalid
        if END in current_dict:
            # If END is found, this string is a full word in our original dictionary
            return TrieMembership.word
        else:
            # If all letters are still in the trie, but this is not a full word,
            # it means there are words that start with this string.
            return TrieMembership.prefix

Traversing the Grid

Friendly Neighbors

For consistency, each square will have and x and a y coordinate. The origin will be in the top left, with x going horizontal and y being vertical. To traverse the grid, you’ll need to know which coordinates are legal targets. This function will determine those legal targets. This function does not however, stop you from revisiting squares, that is handled elsewhere.

def neighbors(x, y):
    if not 0 <= x < BOARD_SIZE or not 0 <= y < BOARD_SIZE:
        raise ValueError("square not within board")

    # x is the x index of the supplied square.  To cover squares to
    # the left and right, we should go from x-1 to x+1.  Because
    # the range() function is not inclusive on the upper bound,
    # we'll need to go to x+2.

    # To prevent returning squares that are outside the board, the
    # range should be capped at 0 and BOARD_SIZE.

    lower_x = max(0, x - 1)
    upper_x = min(x + 2, BOARD_SIZE)

    lower_y = max(0, y - 1)
    upper_y = min(y + 2, BOARD_SIZE)

    for nx in range(lower_x, upper_x):
        for ny in range(lower_y, upper_y):
            yield (nx, ny)

Recursive Searching

This is where the magic happens. Through the power of recursion and backtracking, this function traverses the grid, recording words it finds along the way. The function maintains a list of found path, word pairs and spits them out as the search goes.

def recurse_grid(grid, path, current_word, words_trie, found_words):
    # path should be empty on the initial call
    if not path:
        # This is the initial call to ensure that a search
        # starts from each square in the grid.
        for y, row in enumerate(grid):
            for x, letter in enumerate(row):
                for next_result in recurse_grid_internal(grid,
                                                         [(x, y)],
                                                         letter,
                                                         words_trie,
                                                         found_words):
                    yield next_result

        return
    # path is a list of coordinates, so the last one
    # in the list is our current position in the grid
    current_position = path[-1]

    # test to see how our word is contained in the word list
    membership = trie_member(words_trie, current_word)

    # We have found a new word from our list and
    # should yield the current path and the word
    if membership == TrieMembership.word and current_word not in found_words:
        found_words.add(current_word)
        yield (path, current_word)

    # If it's not a full word, but a prefix to one or more words in the
    # list, continue searching by moving to a neighbor
    # and adding that letter to the current word.
    if membership >= TrieMembership.prefix:
        for nx, ny in neighbors(*current_position):
            # the same square can only be used in each word once
            if (nx, ny) not in path:
                new_letter = grid[ny][nx]

                # the Q cube in boggle has QU on it.
                new_letter = new_letter if new_letter != 'q' else 'qu'

                # add the letter on the newest cube to the current word.
                new_word = current_word + new_letter

                # continue recursively searching from the next square.
                for next_result in recurse_grid_internal(grid,
                                                         path + [(nx, ny)],
                                                         new_word,
                                                         words_trie,
                                                         found_words):
                    yield next_result

Sum it all up

Last but not least, this is how the actual score is tallied up. Each word is turned into a number based on it’s length and they are summed up. It’s really not as interesting as the other stuff.

LEN_TO_SCORE = {3: 1,
                4: 1,
                5: 2,
                6: 3,
                7: 5,
                8: 11,
                9: 11,
                10: 11,
                11: 11,
                12: 11,
                13: 11,
                14: 11,
                15: 11,
                16: 11}

total_score = 0
for word in recurse_grid(grid, list(), "", trie, set())):
    total_score += LEN_TO_SCORE[len(word)]

  1. How to find list of possible words from a letter matrix [Boggle Solver] ↩

  2. Solving the Boggle Game - Recursion, Prefix Tree, and Dynamic Programming ↩

  3. Solving Boggle boards at scale ↩

  4. How to create a TRIE in Python ↩

Header image by https://unsplash.com/@mzeketv