Generating Boggle Boards with Genetics

Posted by Andrew on December 16, 2016

Each week, FiveThirtyEight posts a puzzle call the Riddler. On Oct. 21st, this was the Riddler:

What arrangement of any letters on a Boggle board has the most points attainable? Boggle is played with a 4-by-4 grid of letters. Points are scored by finding strings of letters — connected in any direction, horizontally, vertically or diagonally — that form valid words at least three letters long. Words 3, 4, 5, 6, 7 or 8 or more letters long score 1, 1, 2, 3, 5 and 11 points, respectively.

I had a lot of fun solving this puzzle, and I learned a lot as well, so I decided to share. The approach I took was to use a genetic algorithm, which mimics the mechanics of natural selection. In the past, I hadn’t found a good application, but wanted to give it a shot. You shouldn’t need in-depth knowledge of programming, genetics, or Boggle to learn something!

Genetic Algorithm Background

Natural selection is the process where organisms with favourable traits are more likely to reproduce. In doing so, they pass on these traits to the next generation. Over time this process allows organisms to adapt to their environment. This is because the frequency of genes for favourable traits increases in the population. 1

A genetic algorithm is a metaheuristic inspired by the process of natural selection. Genetic algorithms are commonly used to generate high-quality solutions to optimization and search problems by relying on bio-inspired operators such as mutation, crossover and selection. 2

It may not seem obvious at first how this could be used to generate high scoring Boggle boards, but sit tight! Generally, natural selection works via the following process:

  1. Start with a population of possible solutions (population)
  2. Evaluate them to determine which ones are the best (most fit) (fitness)
  3. The most fit individuals survive (selection)
  4. The surviving individuals reproduce (mating)
  5. Random mutations are introduced into the gene pool (mutation)
  6. Repeat 2-5 for many generations.

Ok, now for the fun stuff! Generating all the possible boggle boards would be practically impossible, so let’s pick a smaller number, say a million. If we scored those boards, we should see a wide range of scores. Now let’s take the high scoring boards, and create some new boards by swapping sections of letters amongst them. This leaves us with some new boards that have potentially high scoring sections in them. Lastly, let’s change a few letters randomly to keep things fresh. Additionally, this may open some new avenues for higher scores. As this process continues, low scoring boards should be eliminated and only high scoring ones will remain (hopefully).

P.S.: If you would like a semi-modern example of natural selection, check out the peppered moth.

Code

The code for this simulation can be found here. Python 3.5, the deap toolbox and matplotlib were the tools used.

Population

A population is a group of organisms of the same species, in a particular area, that are capable of reproducing. For example, this could be a species of birds on an island, or a species of tree in a forest. Within the population, an individual’s physical traits are controlled by their genome. Genomes are broken down into genes, which combine to control the physical traits of the individual. You may be familiar with some traits that are controlled by genes, such as eye color, hair color and blood type.

For our population it makes sense to just have a whole bunch of boards. Unlike nature, we have complete control over the number of individuals and the initial population. We are seeking the highest scoring individual board, so it makes sense for the population to be a large group of boards. The larger the population, the more potential areas that could be explored, with the limiting factor being computation time.

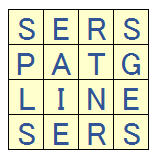
Here is an example individual:

And here's an example population:

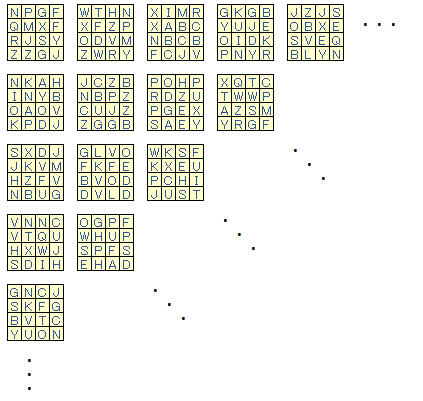
Each board can be represented by a 16 character string, e.g. SERSPATGLINESERS. This string can be thought of as our individual’s genome, and each individual letter can be thought of as a gene. We will be manipulating the genes to get new individuals.

Because we don’t know what kind of solution we might get, the initial population will be created randomly. Once the population is created, we need to determine which solutions should survive and reproduce.

Fitness

In the natural world, each individual does not have an equal chance to pass their genes onto the next generation. Fitness is the term to describe the probability that an individual will contribute to the genes of subsequent generations. Individuals that have the best chance of reproducing are the most “fit” (hence, “survival of the fittest”). The most fit individuals are not necessarily the strongest, fastest or biggest. For example, a particular gene that controls coloring could have a sizable impact on reproduction if it provides great camouflage.

In the natural world, fitness is not as obvious as a single number. One great thing about our problem is that Boggle boards can be scored easily, which gives each board a very clear fitness value. Our fitness function will be the total score of all possible words in the board. After all, this is the goal of the puzzle, so it makes sense to try to maximize this value.

The actual function to perform the scoring is probably worthy of a post in itself, however I think it would be too big of an aside. It can be found in the code here.

Here's an animation showing a particular board being solved:

Selection

Once the population has been evaluated for fitness, some of the individuals will reproduce to create the next generation. In nature, the individuals that would breed would be based on their fitness, mainly the ones that survive and attract a mate. For this problem, we’ll be using tournament selection34. In tournament selection, several individuals are pulled randomly from the population, where they participate in a “tournament”. One individual is picked from the tournament, and individuals with higher fitness are more likely to be picked.

Mating

In order to pass on the genes that lead to their success, individuals must mate. In nature, this takes on many different forms, but ultimately results in a new genome which is a combination of the parents’ genome. For our algorithm, this is done via two point crossover5. Two point crossover selects two points along the genome and then swaps the intermediate sections to create two new chromosomes.

6

In our algorithm, this may look like this:

Mutation

Random mutations are the second mechanism for introducing changes into the population. After the offspring has been produced, small mutations are introduced into the population. Naturally this occurs through errors in DNA reproduction and damage to the DNA sequence. An example of this is Charles Darwin’s finches. In the Galapagos Islands, Darwin discovered that many seemingly similar finches were actually different species. These different species had developed many different beak shapes that allowed them access to new food sources. Some beaks are sharp and pointed to catch insects, while others are broad to better eat seeds from cacti. As these beaks developed, it gave each species access to the new food source, and a better chance of survival.

7

Algorithmically, there are many ways to approach this, but the mutation must be explicitly defined. I’ve chosen to give each letter a small probability to mutate into another random letter. The aggressiveness of the mutation depend on the probability. It’s likely there are other mutations that would work as well, including swapping letters, or additionally shifting letters. Because there is no meaningful link between letters, I chose to mutate the letter randomly.

Solution

Gathering this all together, 1 million boards were generated and evolved over 100 generations. Without specific knowledge about what makes a high scoring Boggle board, we’ve been able to find some very high scoring boards! Likely next steps would be to continue to refine the parameters and probabilities used to further optimize the result. For now though, I’m pretty happy with the result. The final board has a score of 3001:

Here is how the boards evolved over the generations:

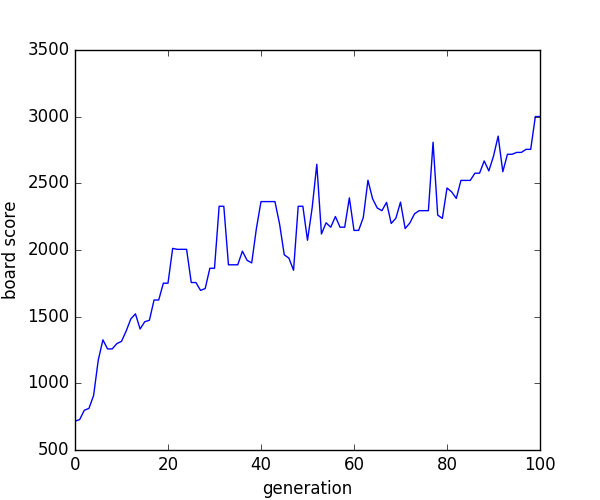
And here are all of the generations:

More solutions can be seen at the end of the Oct. 28th Ridder.

References

  1. https://simple.wikipedia.org/wiki/Natural_selection ↩

  2. https://en.wikipedia.org/wiki/Genetic_algorithm ↩

  3. https://en.wikipedia.org/wiki/Tournament_selection ↩

  4. http://deap.readthedocs.io/en/master/api/tools.html#deap.tools.selTournament ↩

  5. https://en.wikipedia.org/wiki/Crossover_(genetic_algorithm)#Two-point_crossover ↩

  6. By R0oland - Own work, CC BY-SA 3.0, Link ↩

  7.  ↩

Header image by Wellcome Images CC BY 4.0, via Wikimedia Commons